本系列笔记为作者在跟随labuladong的算法小抄学习的时候结合golang做的笔记。感谢东哥。另外根据东哥对算法的分类法,将自己平时记的笔记也写到这里面。
第零章:核心框架汇总
双指针技巧
秒杀链表和数组题目,快慢指针,左右指针
当你需要创造一条新链表的时候,可以使用虚拟头结点简化边界情况的处理
创建链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
type node struct {
val int
next *node
}
func buildList(s []int) *node {
dummy := &node{}
cur := dummy
for _, v := range s {
cur.next = &node{
val: v,
}
cur = cur.next
}
return dummy.next
}
|
展示链表
1
2
3
4
5
6
7
|
func show(head *node) {
cur := head
for cur != nil {
fmt.Println(cur.val)
cur = cur.next
}
}
|
反转链表的某个区间
[l,r)区间,l,r为*ListNode
1
2
3
4
5
6
7
8
9
10
11
12
13
|
l:=k.Next
//l是反转起点
prev,current,next:=nil,l,nil
//终止条件,即反转中点的下一个节点
for current!=r{
next:=current.Next
current.Next=prev
prev=current
current=next
}
//此时current为r,prev为r前一个节点,也是反转后的第一个节点
k.Next=prev
l.Next=current
|
封装成函数
1
2
3
4
5
6
7
8
9
10
11
12
|
reverseK:=func (current *ListNode) (Start,Last *ListNode){
Last=current
var prev *ListNode=nil
for i:=0;i<k;i++{
next:=current.Next
current.Next=prev
prev=current
current=next
}
Start=prev
return
}
|
最长回文子串
中间往两边扩展
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
func longestPalindrome(s string) string {
if s == "" {
return ""
}
ss=s
ll=len(s)
ml, mr := 0, 0
for i := 0; i < ll; i++ {
l1, r1 := expand(i, i)
l2, r2 := expand(i, i + 1)
if r1 - l1 > mr - ml {
ml, mr = l1, r1
}
if r2 - l2 > mr - ml {
ml, mr = l2, r2
}
}
return ss[ml:mr+1]
}
var ss string
var ll int
func expand(l, r int) (int, int) {
for l>=0&&r<ll&&ss[l] == ss[r]{
l--
r++
}
return l + 1, r - 1
}
|
排序
快速排序框架
这里partition是可以通过修改大于小于来选择从大到小或从小到大的排序方式,其他的不用边,下面的代码逻辑是从小到大排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func sort(s []int,l int,r int){
// 通过交换元素构建分界点 p
p:=partition(s,l,r)
sort(s,l,p-1)
sort(s,p+1,r)
}
func partition(s []int,l int,r int)int{
tmp:=s[l]
for l<r{
for l<r&&s[r]>=tmp{r--}
s[l]=s[r]
for l<r&&s[l]<=tmp{l++}
s[r]=s[l]
}
s[l]=tmp
return l
}
|
归并排序框架
1
2
3
4
5
6
7
8
|
func sort(s []int,l int,r int){
mid:=l+(r-l)/2
sort(s,l,mid)
sort(s,mid+1,r)
merge(s,l,mid,r)
}
|
堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
// 向上构建
func Up(s []int, i int) {
if i <= 0 {
return
}
p := (i - 1) / 2
if s[p] < s[i] {
s[p], s[i] = s[i], s[p]
}
Up(s, p)
}
// 向下构建
func Down(s []int, i, l int) {
son1, son2 := i*2+1, i*2+2
if son1 > l {
return
}
max := i
if son1 < len(s) && s[max] < s[son1] {
max = son1
}
if son2 < len(s) && s[max] < s[son2] {
max = son2
}
if i == max {
return
}
s[i], s[max] = s[max], s[i]
Down(s, max, l)
}
// 从第一个非叶子节点构建大顶堆
func BuildHeap(s []int) {
i := (len(s) - 1) / 2
l := len(s) - 1
for i >= 0 {
Down(s, i, l)
i--
}
}
func HeapSort(s []int) {
BuildHeap(s)
l := len(s) - 1
// 根据大顶堆性质进行排序,每次选择最大的放到最后
for l >= 0 {
s[0], s[l] = s[l], s[0]
Down(s, 0, l)
l--
}
}
|
二叉树
1
2
3
4
|
type node struct {
val int
l, r *node
}
|
创建树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
func build(s []int) *node {
cur := 0
var dfs func() *node
dfs = func() *node {
if cur >= len(s) {
return nil
}
if s[cur] == -1 {
cur++
return nil
}
root := &node{
val: s[cur],
}
root.l = dfs()
root.r = dfs()
cur++
return root
}
return dfs()
}
|
展示树
1
2
3
4
5
6
7
8
9
|
func show(root *node) {
if root == nil {
fmt.Println(-1)
return
}
fmt.Println(root.val)
show(root.l)
show(root.r)
}
|
中后序框架
1
2
3
4
5
6
7
8
9
|
func traverse(root *TreeNode){
if root==nil{return}
//前序位置
traverse(root.Left)
//中序位置
traverse(root.Right)
//后序位置
}
|
层序遍历
使用一个list辅助,go里可以使用slice的append内置函数和子切片简单实现,但是并不建议这样做,会造成内存泄露,可以使用container.list,使用也很简单
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
func levelTraverse(root *TreeNode){
if root==nil{return}
q:=[]*TreeNode{root}
for len(q)!=0{
tmp:=q[0]
//处理
q=q[1:]
q=append(q,tmp.Left,tmp.Right)
}
}
//container/list
func levelTraverse(root *TreeNode){
if root==nil{return}
q:=list.New()
for q.Len()!=0{
tmp:=q.Remove(q.Front()).(*TreeNode)
q.PushBack(tmp.Left)
q.PushBack(tmp.Right)
}
}
|
动态规划
动态规划就是聪明的穷举
「最优子结构」:能够只通过子问题的最值得到原问题的最值
「重叠子问题」:子问题存在重复计算,相当于递归树上有相同的节点,使用「备忘录」或者「DP table」来优化(具备这个性质的问题即使没有最优子结构性质,依然可以用备忘录来加速解题过程)
明确 base case(问题的最简单形式) -> 明确「状态」(问题的描述)-> 明确「选择」 -> 根据选择得到从子问题父问题的状态转移方程
定义状态时注意状态要有「无后效性」:已经求解的子问题不受后续阶段的影响
通常DP可以分为两类:自顶向下的动态规划(递归函数实现),自底向上的动态规划(递推算法)。两种方法是同时存在的,并且都需要DP Table优化,它们的状态转移方程是统一的。
这里的选择是修改问题状态的动作,其实就是状态转移方程求最值的参数,每个参数都是一个选择,表示父问题如何从子问题的结果得到自己的结果。比如股票买卖就是我今天是否卖出,买卖就是选择
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
var dp_table [状态1][状态2][...]
//状态初始化
func init(){}
//自顶向下
func dp(i,j){
for 选择 in 所有可能的选择:
result = 求最值(result,从子问题选择后的结果)
}
//自底向上
func solution(){
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
...
dp[状态1][状态2][...] = 求最值(所有选择的结果)
}
|
对于特定遍历顺序的DP可以进行空间优化,比如状态转移方程每次只需要2个子问题的状态,那么就可以把不需要的状态丢弃,仅保持最新的子问题状态
将一个维度分为多个状态转移方程时,这些状态转移方程在一轮中执行,且该维度不用进行遍历了
维度遍历顺序和遍历方向以及初始化值依据等式右边该维度的值:
- 都是i-k(i+k),遍历方向为从小到大(从大到小),初始化i=0(i=max)
- 都是i-k(i+k)和i,遍历方向为从小到大(从大到小),初始化i=0(i=max)
- 有i-k和i+k,遍历方向不限,初始化i的所有取值
对于边界条件可以在状态转移方程中修改一下逻辑,比如添加一个if判断,是边界值是直接continue或者是其他逻辑
回溯法
回溯法解决所有的排列,组合,子集问题
回溯的关键是选择
回溯其实就是暴力,有时候可以通过备忘录剪枝,但是一般情况都不存在重叠子问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
ans:=[]int
onpath:=[]int
visited:=[]bool
func backtrack(当前位置){
if 满足条件{
ans=append(ans,onpath)
return
}
for 选择 := 当前位置.选择列表{
做选择(添加当前位置)
backtrack(选择后的位置)
撤销选择(取消当前位置)
}
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
var ans *Node
func BFS(root *Node,target int){
q:=[]*Node{root}
for len(q)!=0{
tmp:=q[0]
q=q[1:]
if tmp满足条件{
tmp处理
}
c:=tmp.children
for i:=0;i<len(c);i++{
q=append(q,c[i])
}
}
}
|
对于需要避免走回头路的可以使用map或者数组来标记visited
二分搜索
寻找一个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
func binarySearch(s []int,t int)int{
l,r,mid:=0,len(s)-1,0
for l<=r{
mid=l+(r-l)/2
if s[mid]<t{
l=mid+1
}else if s[mid]>t{
r=mid-1
}else{
return mid
}
}
return -1
//找不到时l为插入位置
// return l
}
|
寻找左侧边界的二分搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func left_bound(s []int,t int)int{
l,r,mid:=0,len(s)-1,0
for l<=r{
mid=l+(r-l)/2
if s[mid]<t{
l=mid+1
}else if s[mid]>t{
r=mid-1
}else{
//需注意位置,这里改变的是r
r=mid-1
}
}
//需注意位置,往左边找考虑最右边的情况,这里判断l
if l==len(s){return -1}
//需注意位置,这里判断l,如果没找到l是插入位置
if s[l]==t{return l}else{return -1}
}
|
寻找右侧边界的二分查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func right_bound(s []int,t int)int{
l,r,mid:=0,len(s)-1,0
for l<=r{
mid=l+(r-l)/2
if s[mid]<t{
l=mid+1
}else if s[mid]>t{
r=mid-1
}else{
//需注意位置,这里改变的是r
l=mid+1
}
}
//需注意位置,往右边找考虑在最左边的情况,这里判断l-1
if l-1<0{return -1}
//需注意位置,这里判断l-1
if s[l-1]==t{return l-1}else{return -1}
}
|
寻找旋转排序数组的最小值
1
2
3
4
5
6
7
8
9
10
11
12
|
func findMin(nums []int) int {
low, high := 0, len(nums) - 1
for low < high {
pivot := low + (high - low) / 2
if nums[pivot] < nums[high] {
high = pivot
} else {
low = pivot + 1
}
}
return nums[low]
}
|
滑动窗口
重要,左闭右开
1
2
3
4
5
6
7
8
9
|
l,r:=0,0
for r<len(s){
入滑动窗口处理s[r]
r++
for l满足增大条件{
出滑动窗口处理s[l]
l++
}
}
|
单调队列
单调队列是一种特殊的滑动窗口,他保证滑动窗口内的元素具有单调的性质,单调上升或单调下降
1
2
3
4
5
6
7
8
9
|
l,r:=0,0
for r<len(s){
入滑动窗口处理s[r]
r++
for l满足增大条件||s[l]<s[r]{
出滑动窗口处理s[l]
l++
}
}
|
股票买卖
状态:天数i,允许交易最大次数k,持有状态[0,1]
选择:sell,buy,rest
在buy的时候减小k,因为交易是从buy开始的
1
2
3
4
5
|
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 今天选择 rest, 今天选择 sell )
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 今天选择 rest, 今天选择 buy )
|
时空复杂度分析
Big O 表示法
O(g(n))= {f(n): 存在正常量c和n_0,使得对所有n ≥ n_0,有0 ≤ f(n) ≤ c*g(n)}
- 只保留增长速率最快的项,其他的项可以省略
- Big O 记号表示复杂度的「上界」
非递归算法分析
空间复杂度:分配的数组空间大小
时间复杂度:循环相乘,顺序相加,取最大的加数
数据结构分析
摊还(平均)时间复杂度:算N个操作总的时间复杂度然后除以N
比如一个单调栈,每个元素都进栈出栈一次,所以总的时间复杂度是O(2N),除以N就是O(2),取常数复杂度所以是O(1)
递归算法分析
递归算法的时间复杂度 = 递归树的节点个数 x 每个节点的时间复杂度
递归算法的空间复杂度 = 递归树的高度(递归栈的空间消耗) + 算法申请的存储空间
解法代码分层
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
//解题函数
func getans(nums []int){
//数据初始化
a,l=0,len(nums)
b=make([]slice,l)
//委托solution求解
solution(nums)
return ans
}
//全局变量
var (
a int
l int
b []int
ans int
)
//solution函数,该函数也可以内联到解题函数中
func solution(nums []int){
//具体算法
}
//工具函数,如递归
func traverse(){
//具体算法
}
|
递归Debug
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
//全局变量
var count int
func printIndent(n int){
for i:=0;i<n;i++{fmt.Print(" ")}
}
func dp(){
count++
//每个fmt.println()之前调用printIndent(count)
printIndent(count)
fmt.Println(xxx)
count--
}
|
一个方法解决n和问题
2和问题,排序+对撞指针
n和问题,排序+穷举(减小问题规模)+对撞指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
func KSum(nums []int, target int,k int) [][]int {
l:=len(nums)
sort.Ints(nums)
onpath:=make([]int,0,k-2)
ans:=make([][]int,0)
var rec func (int,int,int)
rec=func (i,t,n int){
//fmt.Println(onpath,len(onpath),n)
if i>=l{return}
if n==2{
left,right:=i,l-1
for left<right{
if nums[left]+nums[right]<t{
left++
for left<right&&(left==0||nums[left]==nums[left-1]){left++}
}else if nums[left]+nums[right]>t{
right--
for right>left&&(right==l||nums[right]==nums[right+1]){right--}
}else{
tmp:=make([]int,k-2,k)
copy(tmp,onpath)
tmp=append(tmp,nums[left],nums[right])
ans=append(ans,tmp)
left++
right--
for left<right&&(left==0||nums[left]==nums[left-1]){left++}
for right>left&&(right==l-1||nums[right]==nums[right+1]){right--}
}
}
}else {
for i<l{
onpath=append(onpath,nums[i])
rec(i+1,n-1,t-nums[i])
onpath=onpath[:len(onpath)-1]
i++
for i<l&&(i==0||nums[i]==nums[i-1]){i++}
}
}
}
rec(0,target,k)
return ans
}
|
n数之和只需要将n传递给函数中的k即可
第一章:手把手刷数据结构
前缀和数组
频繁查询某个区间的累加和
1
2
3
4
5
6
7
8
9
|
var preSum []int
//构造过程也可以内联到解题函数中
func NumArray(s []int){
preSum=make([]int,len(s)+1)
for i:=1;i<len(preSum);i++{
preSum[i]=preSum[i-1]+s[i-1]
}
}
|
差分数组
快速进行区间增减的操作
1
2
3
4
5
6
7
8
9
10
|
var diff []int
//构造过程也可以内联到解题函数中
func NumArray(s []int){
diff=make([]int,len(s))
diff[0]=s[0]
for i:=1;i<len(diff);i++{
diff[i]=s[i]-s[i-1]
}
}
|
常数时间删除-查找数组中的任意元素
解决办法:valToIndex哈希表+数组
常数时间删除:哈希表查询索引,数组中将该索引与最后一个元素互换,删除最后一个元素,哈希表修改最后一个元素的键值对并删除被删索引的键值对
常数时间查询:哈希表查询索引,数组随机访问
最近公共祖先(Lowest Common Ancestor,简称 LCA)
1
2
3
4
5
6
7
8
9
10
|
func find(root *TreeNode,t1 int,t2 int)*TreeNode{
if root==nil{return nil}
if root.Val==t1||root.Val==t2{return root}
l:=find(root.Left,t1,t2)
r:=find(root.Right,t1,t2)
if l!=nil&&r!=nil{return root}
if l!=nil{return l}else{return r}
}
|
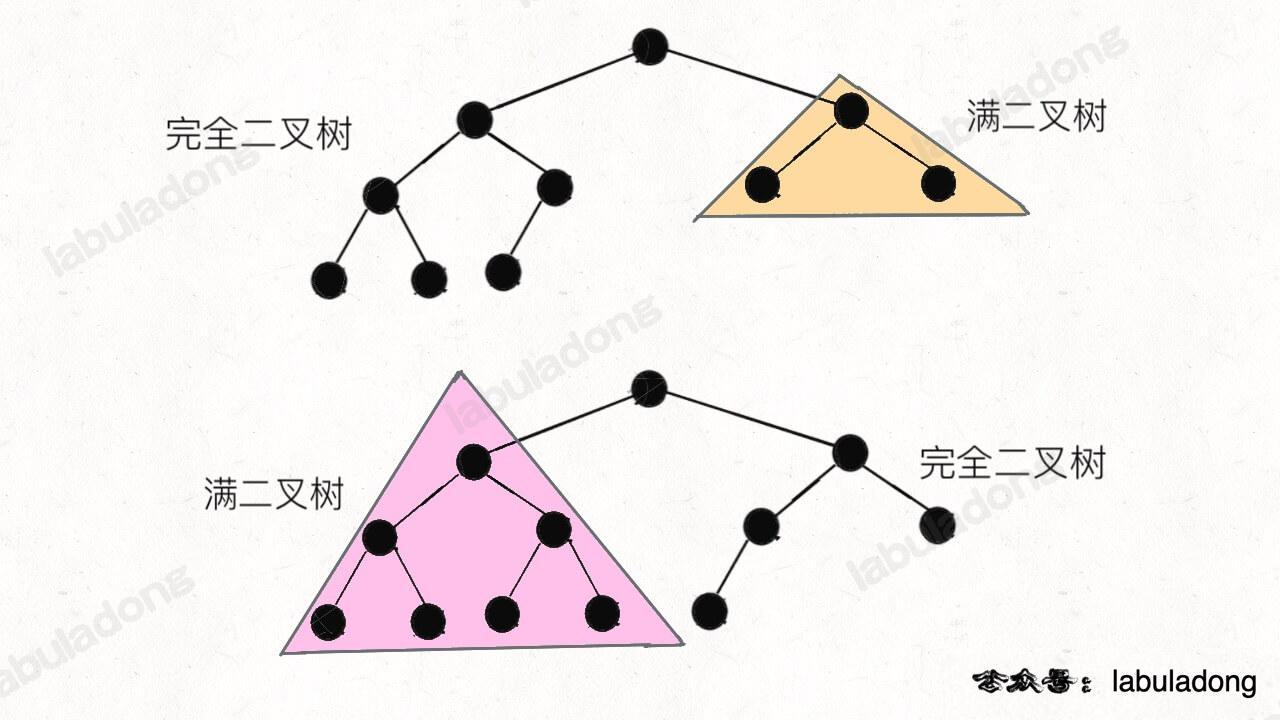
计算完全二叉树的节点数
一棵完全二叉树的两棵子树,至少有一棵是满二叉树,满二叉树的节点数为2^h-1个(h为树高,root为第1层)
时间复杂度 O(logN*logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
func countNodes(root *TreeNode){
l,r,hl,hr,ret:=root,root,0,0,0
for l!=nil{
hl++
l=l.Left
}
for r!=nil{
hr++
r=r.Right
}
if hl==hr{
ret=1<<hl-1
}else{
ret=1+countNodes(root.Left,root.Right)
}
return ret
}
|
多叉树遍历
1
2
3
4
5
6
7
8
9
10
11
|
func traverse(root *TreeNode){
if root==nil{return}
//先序处理
c:=root.Children
for i:=0;i<len(c);i++{
traverse(c[i])
}
//后序处理
}
|
DFS图遍历(仅展示邻接表,通常都是邻接表,[][]int)
多叉树基础上添加visited数组和onpath数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
var (
visited []bool
onpath []bool
l int
)
//初始化过程也可以内联到解题函数中
func init(graph [][]int){
l=len(graph)
visited=make([]bool,l)
onpath=make([]bool,0,l)
}
func tarverse(graph [][]int,n int){
if visited[n] {return}
visited[n]=true
onpath[n]=true
//前序处理位置
c:=graph[n]
for i:=0;i<len(c);i++{
traverse(c[i])
}
//后序处理位置
onpath=false
}
for traverseGraph(graph [][]int){
init(graph)
for i:=0;i<l;i++{
traverse(i)
}
}
|
环检测
DFS
修改图遍历中的traverse函数,添加hascycle全局变量(go中bool零值为false)
1
2
3
4
5
6
7
8
9
|
var hascycle bool
func tarverse(graph [][]int,n int){
if onpath[n]{hascycle=true}
if visited[n]||hascycle {
return
}
...
}
|
当题目给的是边的序列和节点总数时使用建图函数:
1
2
3
4
5
6
7
8
9
10
11
12
|
var graph [][]int
func buildGraph(edge [][]int,l int){
graph=make([][]int,l)
for i:=0;i<l;i++{
graph[i]=make([][]int,0)
}
for i:=0;i<len(edge);i++{
graph[edge[i][0]]=append(graph[edge[i][0]],edge[i][1])
}
}
|
BFS
添加入度数组indegree,建图函数修改
1
2
3
4
5
6
7
8
9
10
|
var indegree []int
func buildGraph(){
...
indegree = make([]int,l)
for i:=0;i<len(edge);i++{
graph[edge[i][0]]=append(graph[edge[i][0]],edge[i][1])
indegree[edge[i][1]]++
}
}
|
使用一个队列将入度为0的节点放入队列中,每取一个节点就把依赖该节点的其他节点入度减1,然后把入度为0的未访问过节点加入队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
func canFinish(){
ans:=make([]int,0,l)
list:=make([]int,0,l)
for i:=0;i<l;i++{
if indegree[i]==0{list=append(list,i)}
}
for len(list)>0{
c:=graph[list[0]]
list=list[1:]
for i:=0;i<len(c);i++{
indegree[c[i]]--
if indegree[c[i]]==0{
list=append(list,c[i])
}
}
}
for i:=0;i<l;i++{
if indegree[i]!=0{
hascycle=true
break
}
}
return hascycle
}
|
拓扑排序
DFS
图DFS后序遍历的序列反转就是拓扑排序
后续遍历等子节点都装到序列后才装父节点,所以它的反转就是父节点都装到序列后再装子节点,这个正好是拓扑排序的定义:一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行。
需要配合环检测,有环的图不能进行拓扑排序,所以在返回结果前需要判断是否有环
BFS
与环检测一样,在每次弹出list[0]之前将list[0]加入ans数组
二分图判定
图DFS遍历,遍历过程中染色节点,当visited为true时不直接返回,而是进行判断是否染色冲突
并查集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
type UF struct{
parent []int //父节点数组
count int //连通分量数
}
func NewUF(n int) *UF{
ret:=&UF{}
ret.count=n
ret.parent=make([]int,n)
for i:=0;i<n;i++{
ret.parent[i]=i
}
return ret
}
func (uf *UF)Find(x int)int{
if uf.parent[x]!=x{
//路径优化
uf.parent[x]=uf.Find(uf.parent[x])
}
return uf.parent[x]
}
func (uf *UF)Union(p,q int){
rootP:=uf.Find(p)
rootQ:=uf.Find(q)
if rootP==rootQ{return}
uf.parent[rootQ]=rootP
uf.count--
}
func (uf *UF)Connected(p,q int)bool{
rootP:=uf.Find(p)
rootQ:=uf.Find(q)
return rootP==rootQ
}
func (uf *UF)Count()int{
return uf.count
}
|
带权UF可以添加一个数组来记录权值,并修改Find和Union里面的逻辑以维护权值
1
2
3
4
5
6
7
8
9
10
11
|
func validTree(n int,edges [][]int)bool{
uf:=NewUF(n)
for i:=0;i<len(edge);i++{
u,v:=edges[i][0],edges[i][1]
if uf.connected(u,v){
return false
}
uf.Union(u,v)
}
return uf.Count()==1
}
|
KRUSKAL 最小生成树算法
边权值贪心
结合并查集环检测算法和边权重排序,这里边为一个形式为[from,to,weight]的int数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func minimumCost(n int,connections [][]int){
uf:=NewUF(n+1)
sort.Slice(connections,func (i,j int){
return connections[2]<connection[2]
})
//最小权重和
mst:=0
for edge:=range connections{
u,v,w:=edge[0],edge[1],edge[2]
if uf.Connected(u,v){
continue
}
mst+=w
uf.Union(u,v)
}
//节点0未使用,所以是2
if uf.Count()==2{
return mst
}
return -1
}
|
PRIM 最小生成树算法
切分贪心
切分定理
切分:将一幅图分为两个不重叠且非空的节点集合
切分定理:对于任意一种「切分」,其中权重最小的那条「横切边」一定是构成最小生成树的一条边
PRIM算法
见原文
DIJKSTRA 算法
从某个点开始带优先级的BFS,查询从开始节点到其他节点的最短路径和最小路径和
见原文
单调栈
单调递增
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
type S []int
func (s *S)Pop()int{
l:=len(*s)
if l<0{return -1}
ret:=(*s)[l-1]
*s=*s[:l-1]
return ret
}
func (s *S)Push(x int){
l:=len(*s)
for s[l-1]>x&&l!=0{
s.Pop()
l--
}
*s=append(*s,x)
}
|
自己总结的模板,单调递增
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
l:=len(heights)
stack:=make([]int,0,l)
chuliluoji:=func(i,x int){
...
}
for i,v:=range heights{
x:=...
for len(s)>0&&s[s[len(s)-1]]>v{
chuliluoji(i,x)
s=s[:len(s)-1]
}
s=append(s,i)
}
x:=...
for len(s)>0{
chuliluoji(l,x)
s=s[:len(s)-1]
}
|
优先队列
注意,只有结构体里面的匿名字段能继承方法,类型定义别名无法继承方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
type PriorityQueue struct {
sort.IntSlice
}
func (h *PriorityQueue) Push(x interface{}) {
h.IntSlice = append(h.IntSlice, x.(int))
}
func (h *PriorityQueue) Pop() interface{} {
l := len(h.IntSlice)
if l==0{
return 0
}
ret := h.IntSlice[l-1]
h.IntSlice = h.IntSlice[:l-1]
return ret
}
func (h *PriorityQueue) HPush(x int) { heap.Push(h, x) }
func (h *PriorityQueue) HPop() int { return heap.Pop(h).(int) }
|
最短路径:BF,SPFA和Floyd算法
BF松弛算法
单源最短路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
var graph [][]int
var minPath []int
var preNode []int
var l
func bfs(s int)bool{
minPath,preNode=make([]int,l),make([]int,l)
for i:=0;i<l;i++{
minPath[i]=math.MaxInt
preNode[i]=-1
}
minPath[s]=0
//松弛l-1轮
for i:=0;i<l-1;i++{
//每轮松弛所有边
for u:=0;u<l;u++{
for _,V:=range graph[u]{
v,w:=V[0],V[1]
tmp:=Add(minPath[u],w)
if minPath[v]>tmp{
minPath[v]=tmp
preNode[v]=u
}
}
}
}
//松弛第l轮,如果还有改变表示有负环,返回错误
for u:=0;u<l;u++{
for _,V:=range graph[u]{
v,w:=V[0],V[1]
tmp:=Add(minPath[u],w)
if minPath[v]>tmp{
return false
}
}
}
return true
}
func Add(a,b int){
if a==math.MaxInt||b==math.MaxInt{return math.MaxInt}
return a+b
}
|
SPFA算法
BF队列优化,额外需要一个记录顶点入队次数的数组(不能超过l-1次,每条边松弛不超过l-1次)。使用优先队列还能进行优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
import aq "github.com/emirpasic/gods/queues/arrayqueue"
var graph [][]int
var minPath []int
var preNode []int
var eqTime []int
var l
func spfa(s int)bool{
minPath,preNode,eqTime=make([]int,l),make([]int,l),make([]int,l)
for i:=0;i<l;i++{
minPath[i]=math.MaxInt
preNode[i]=-1
}
minPath[s]=0
queue := aq.New()
queue.Enqueue(s)
eqTime[s]++
for !queue.Empty(){
u,_:=queue.Dequeue()
for _,V:=range graph[u]{
v,w:=V[0],V[1]
tmp:=Add(minPath[u],w)
if minPath[v]>tmp{
minPath[v]=tmp
preNode[v]=u
queue.Enqueue(v)
//入队次数超过l-1,出现负环,返回错误
eqTime[v]++
if eqTime>=l{
return false
}
}
}
}
return true
}
func Add(a,b int){
if a==math.MaxInt||b==math.MaxInt{return math.MaxInt}
return a+b
}
|
Floyd算法
全源最短路径,使用邻接矩阵,O(n^3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
var graph [][]int
var minPath [][]int
var l int
func floyd(s int)bool{
minPath=make([][]int,l)
for i:=0;i<l;i++{
minPath=make([]int,l)
for j:=0;j<l;j++{
minPath[i][j]=math.MaxInt
}
}
//枚举顶点K
for k:=0;k<l;k++{
//对任意一条路径i,j选k为中点
for i:=0;i<l;i++{
for j:=0;j<l;j++{
tmp:=Add(minPath[i][k],minPath[k][j])
if minPath>tmp{
minPath[i][j]=tmp
}
}
}
}
}
func Add(a,b int){
if a==math.MaxInt||b==math.MaxInt{return math.MaxInt}
return a+b
}
|
KMP
getNextVal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func getNext(p []byte) []int{
i, j, l := 1, 0, len(p)
next = make([]int, l)
for i < l {
if j == 0 || p[i] == p[j] {
next[i] = j
i++
j++
} else {
j = next[j]
}
}
return next
}
|
KMP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func KMP(s []byte, p []byte, next []int) int {
i, j, ls, lp := 0, 0, len(s), len(p)
for i < ls && j < lp {
if j == 0 || s[i] == p[j] {
i++
j++
} else {
j = next[j]
}
}
if j == lp {
return i - lp
} else {
return -1
}
}
|
固定滑动窗口框架
leetcode 2379 得到 K 个黑块的最少涂色次数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func minimumRecolors(blocks string, k int) int {
ans:=math.MaxInt
tmp:=0
//1. 设置两个指针分别指向滑动窗口的两端,左闭右开
i,j,l:=0,0,len(blocks)
//2. 先读取窗口大小的元素
for i<k&&i<l{
if blocks[i]=='W'{tmp++}
i++
}
//3. 进行一次窗口判断
if ans>tmp{ans=tmp}
//4. 窗口移动并进行窗口判断
for i<l{
if blocks[i]=='W'{tmp++}
if blocks[j]=='W'{tmp--}
i++
j++
if ans>tmp{ans=tmp}
}
return ans
}
|
字典树
1
2
3
4
5
6
7
8
9
10
11
|
// 非固定数量child
type Trie struct {
childs map[xxx]*Trie
isEnd bool
}
// 固定数量child
type Trie struct {
childs [n]*Trie
isEnd bool
}
|